Why don’t radio broadcasts interfere with each other?

Radio sets are ancient technology (to me at least), and as such, I never questioned their inner workings.

What you can infer from usage is that radio broadcasts aren’t simply “electromagnetic speakers”. They don’t just transmit audio by sending the raw waves over the air, the same way a speaker would. You’d never receive any clear sound, the same way setting up multiple speakers with different music makes it impossible to listen to anything.

The answer to the enigma is that radio stations use FM (or AM, but less so). You can find these two letters on most radio sets, and I’ll try my best to explain what they are all about.

How does Frequency Modulation work?

Before we venture into sending audio over the air, let’s start with a simpler example. We’ll send a simple sine wave using FM.

To frequency modulate (FM) a signal, start with the carrier signal - a sine wave with a constant frequency, called the carrier frequency. Then, as the name implies, FM encodes information about the amplitude of the signal we sent by **modulating **(shifting) the **frequency **of the carrier signal.

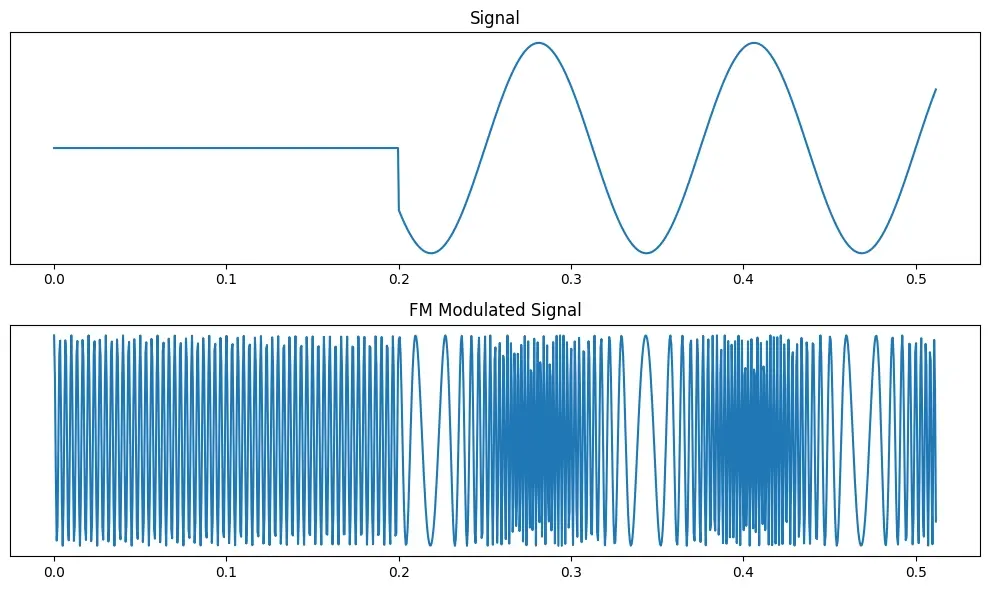
You can see how at the peaks of our message signal, the modulated signal is getting compacted (meaning higher frequencies) and at the troughs, it is getting stretched (meaning lower frequencies).

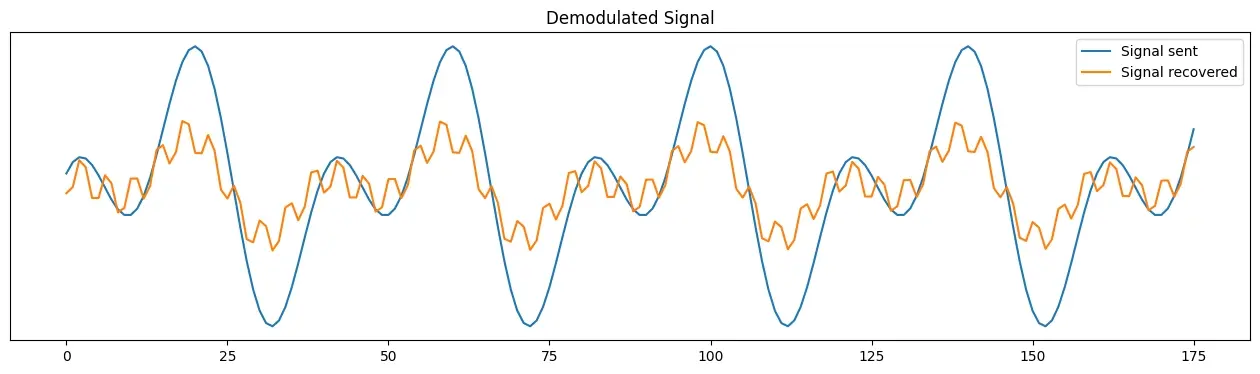
Next, let’s see what sending a more complex message signal looks like. The graph shows that the modulated signal is dilated and contracted the same as before, but what’s happening is less clear to the human eye.

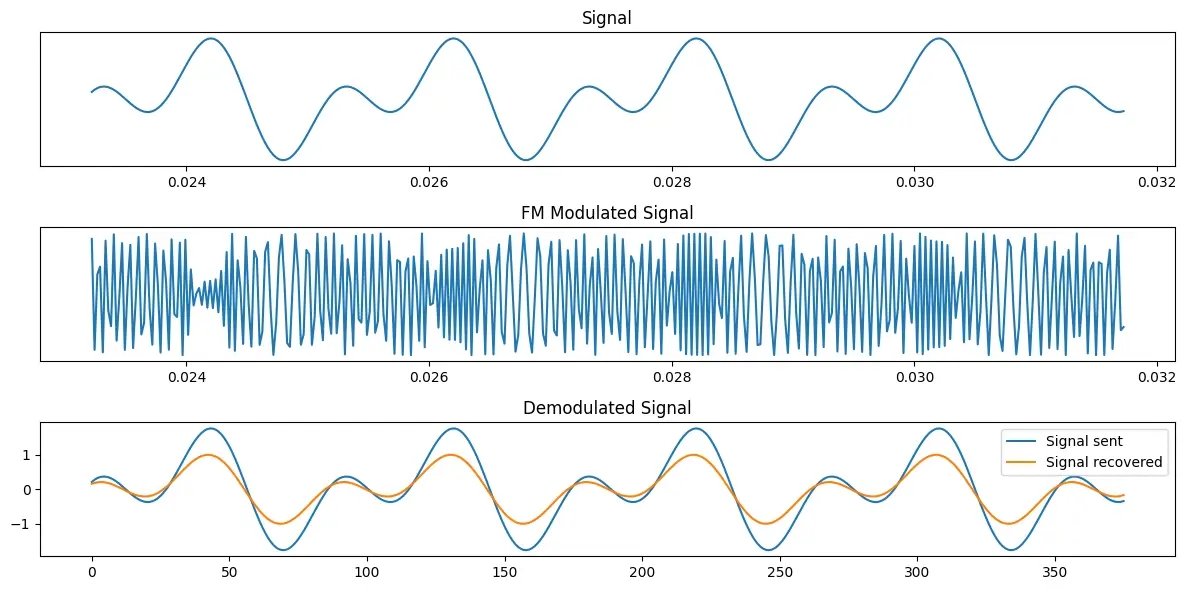
The bottom graph compares our message signal (in blue), the top graph, with what we recover from the FM signal, through demodulation (in orange).

Demodulation

Our goal with demodulation is to reverse the process of frequency modulation: extract the frequency at every point of the FM signal, and thus recover the amplitudes at every point of the original message.

We can use the Hilbert transform, which shifts a signal by 90 degrees. Combining the modulated signal with the result of the Hilbert transform gives us a complex result - the analytical signal. The real part is the modulated signal, the imaginary component the result of the Hilbert transform.

Let’s plot the analytical signal in 3d space, x-axis showing the real part and y-axis the imaginary part.

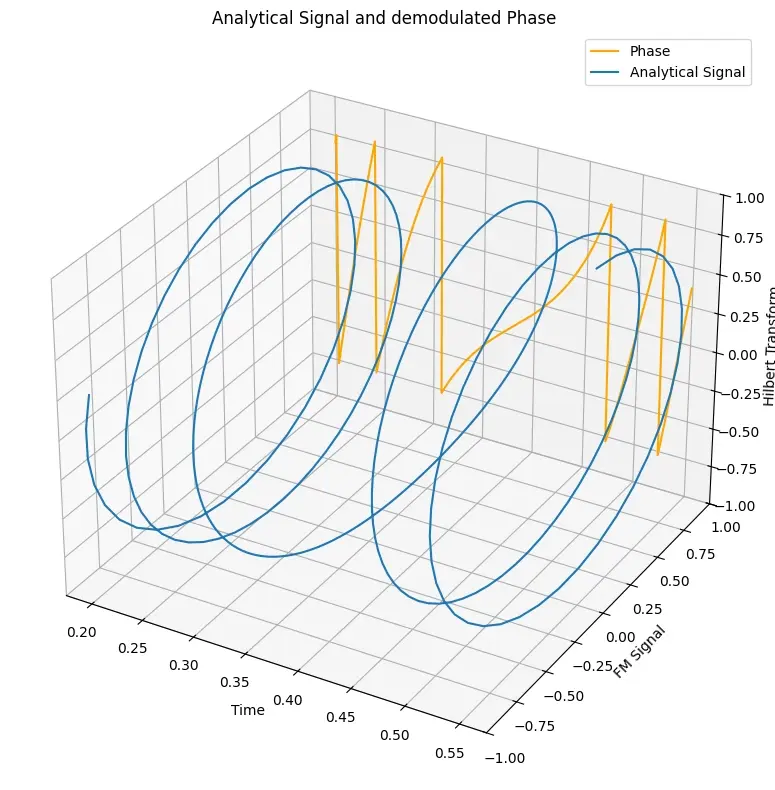
In orange, I’ve plotted the instantaneous phase which we can get from the analytical signal. It’s the angle of the signal in complex space.

The tighter wound the coil of the analytical signal (higher frequency), the steeper the slope of the instantaneous phase curve. A higher slope means Thus, by deriving the instantaneous phase, we can recover the frequency of the signal.

And from that, we can recover our original message, by mapping frequency changes to amplitude. Success, we can listen to radio now!

Multiple Broadcasts

We’ve only treated the case of a single signal being sent before. But to simulate radio stations, we’ll have to deal with multiple broadcasters and thus signals. Now we’re getting to the heart of the question of why radio broadcasts don’t interfere!

We have two parameters to play with: carrier frequency and frequency deviation.

Frequency deviation measures by how much the modulation shifts the carrier frequency. If we broadcast with a carrier frequency of 100 MHz and set our deviation to 1 MHz, the resulting FM signal will vary in frequency from 99-101 MHz. We can’t have a second station broadcasting at 99 MHz or they would interfere. Thus, we have to consider how much of the bandwidth each broadcast is taking up.

Because the air is full of competing signals, we have to “tune-in” - filter out other frequencies - before demodulating. By turning the knobs to 99.9 MHz on the radio set, you’re telling your radio set to filter out everything except 99.9 +/- 1 MHz (if the deviation was 1 MHz).

The combination of choosing the right broadcast parameters and effective filtering makes it possible to listen to a single radio station in the sea of waves that traverse the air.

Limitations and Noise

If we set the frequency deviation too high, the signals will start interfering on shared frequencies, and we won’t be able to separate them again.

The following frequency spectrum shows two radio stations, broadcasting at 8KHz and 18KHz, with a frequency deviation of 4KHz. There’s just enough bandwidth for them not to overlap.

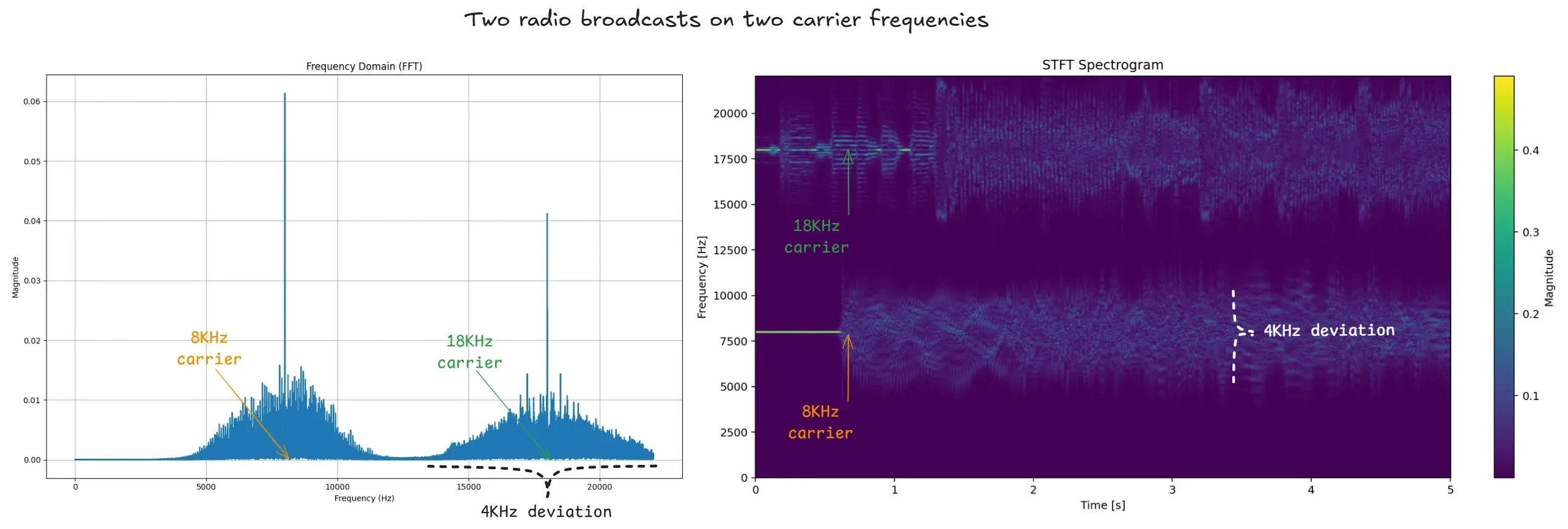
To maximise the amount of channels, you’d want to **reduce **the frequency deviation. This way, you can have more broadcasts on the same bandwidth. But, there is a limiting factor in play here: when the frequency deviation gets too low, the signal is “compressed”.

The smaller the frequency deviation, the smaller the change in frequency to signify the same change in amplitude. At some point, due to a limited sample rate, changes won’t be detectable any more, and you get the noise you see below. As such, the maximum frequency deviation is limited by the “resolution” of the receiver.

Real radio stations broadcast at around 100MHz. The stations are 200KHz apart. The standard frequency deviation of around 75KHz ensures that there is more than enough space for each broadcast, while minimising noise.

Simulating FM radio stations

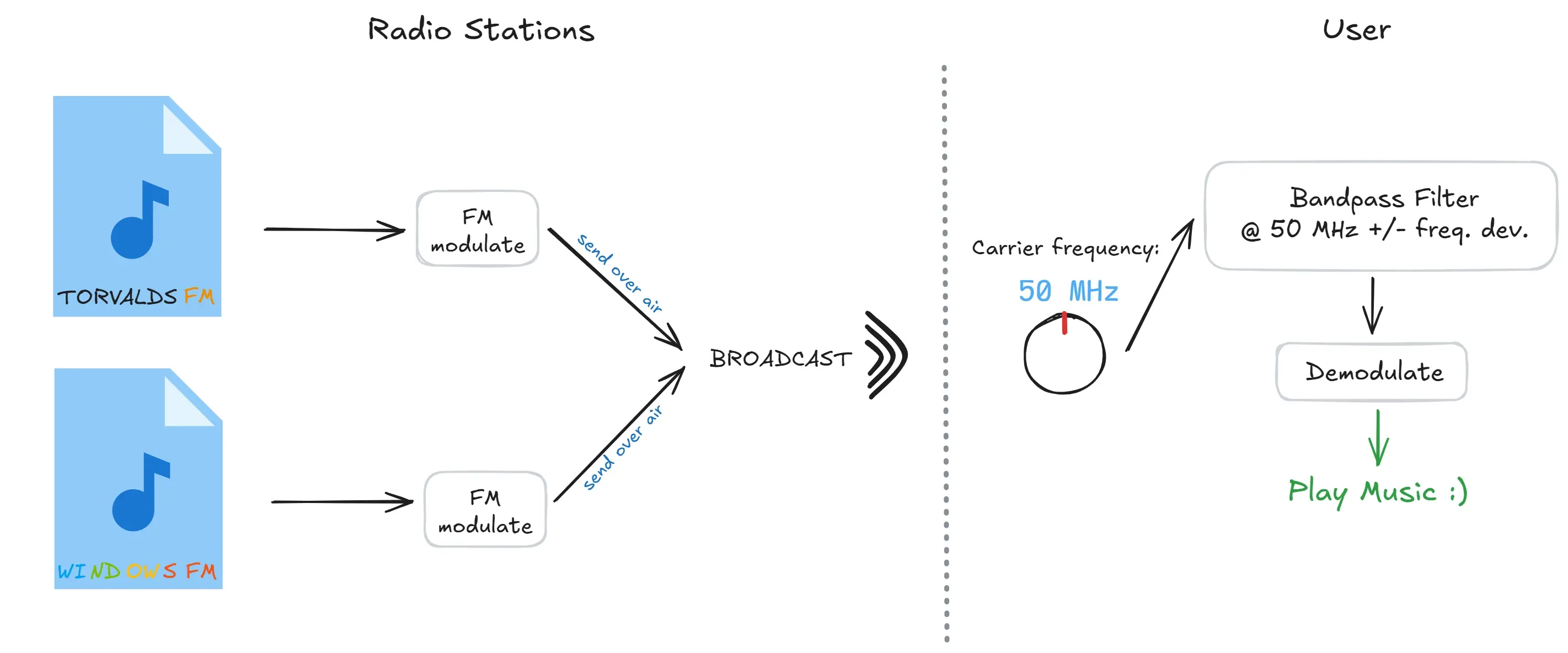
As a proof of concept, I simulated two radio broadcasts, and tried tuning into each of them.

I used numpy to simulate 5 seconds of broadcast at 176.4 KHz (which is 4 times the 44.1 KHz sample rate of standard .wav files), one station at 30 KHz and the other at 60 KHz with a frequency deviation of 10 KHz (which should be enough for them not to interfere).

I determined these settings through some trial and error - especially the frequency deviation, which should be high enough not to be distorted by the “compression”, as explained before.

The main consideration however was choosing a sample rate that allows two stations. To prevent aliasing, the sample rate has to be at least equal to the Nyquist rate, which is twice the highest frequency of the signal. As the highest frequency of audible sound is about 20 KHz, audio recordings have a sample rate of more than 40 KHz (double the bandwidth), for example CDs at 44.1 KHz.

In my simulation, I take two .wav audio files, then re-sample them to match the sample rate. Both are then modulated independently and then their signals are added together, by simple adding both numpy.arrays. This should be an accurate enough model of real signals interfering.

To “tune-in” to one of the stations, I then apply a Butterworth band-pass filter centred around the carrier frequency, plus and minus the frequency deviation. Below is the spectrogram generated from my simulated broadcasts.

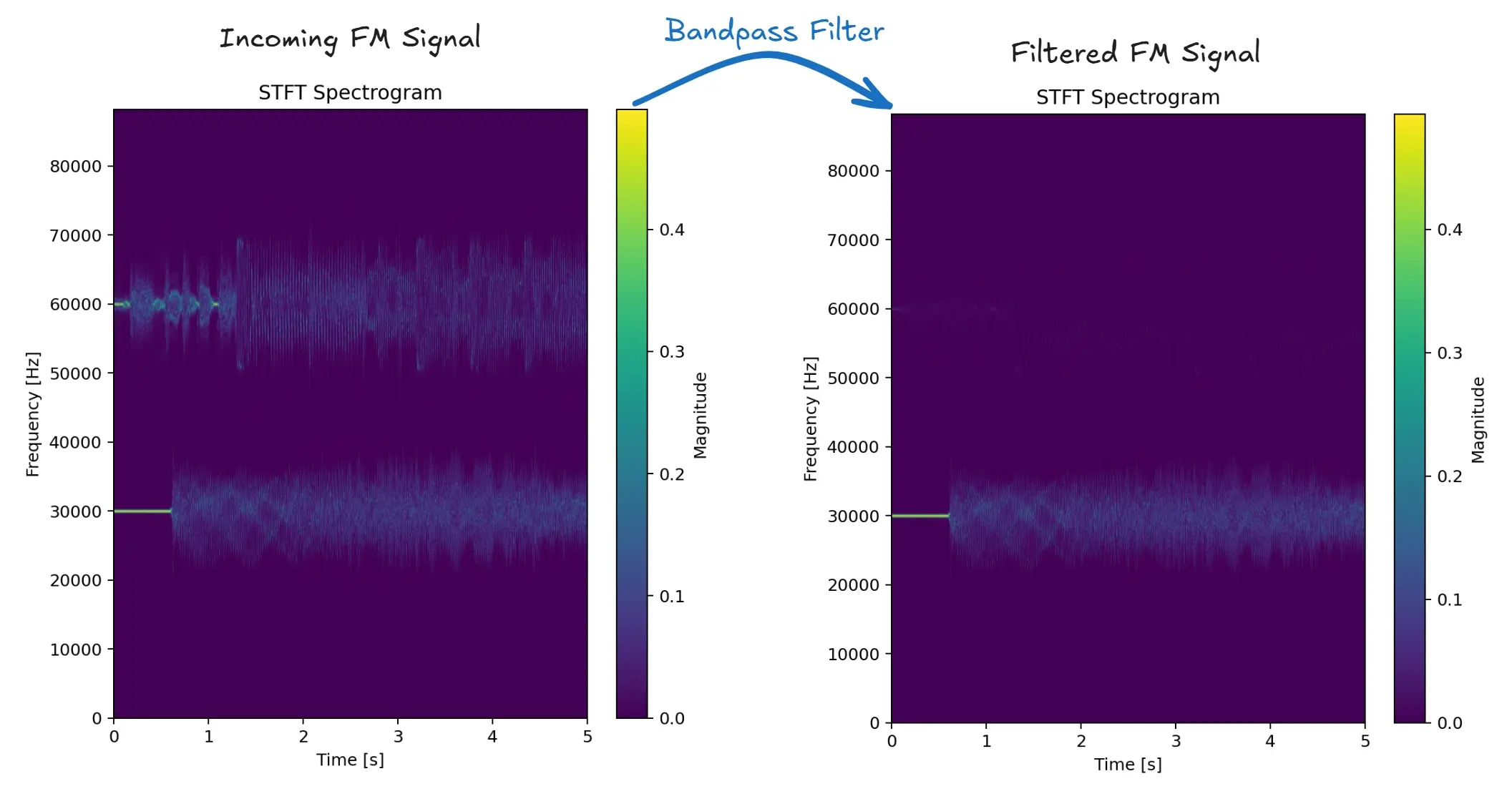
To recover the audio, we apply our demodulation technique, and voilà.

Below are .wav files with: the original audio (1); the demodulated audio with 10 KHz (2) deviation and with 1KHz (3) (to make noise audible); and with carrier frequencies too close together (4), as to make interference audible:

Original

10 KHz deviation

1 KHz deviation

Interfering broadcasts

So why don’t broadcasts interfere?

As you heard in the last audio simple, FM signals do interfere. Radio broadcasts work, because although they do interfere, you can recover the individual frequency bands signal using filters. As real radio stations have well chosen carrier frequencies and deviations, radio broadcasts can be cleanly filtered.

The filtering works because although waves interfere, you can recover the initial “ingredients” by looking at the result. The example below shows a sine wave with 1Hz and one with 5Hz.

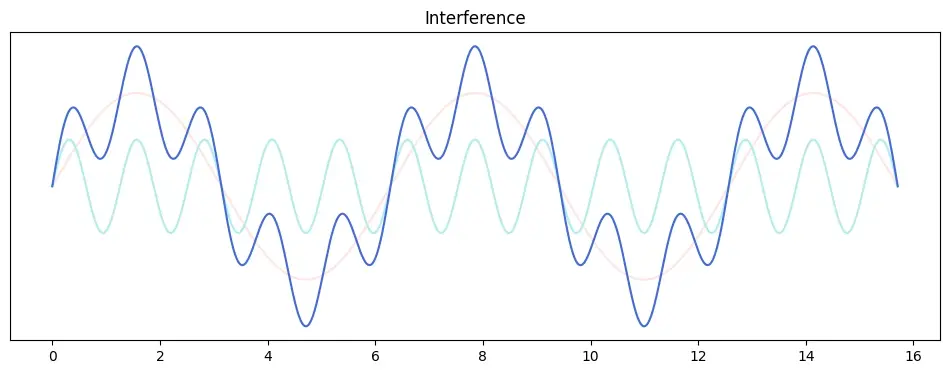
You can still guess that the resulting wave was made by adding one sine wave with a longer and one with a shorter period. Using the FFT you could recover the individual frequencies here. In a radio, an electronic band-pass filters would have the job to let only desired frequencies through.

TL;DR;

Frequency modulation is the basis of most modern communication, from radio to cell coverage, to Wi-Fi and Bluetooth. It encodes a message by slightly shifting (modulating) the frequency of a carrier wave.

To decode the signal and recover the message, the receiver filters out everything except the carrier frequency and maps frequency changes back to the amplitude of the original message.

Please let me know if I’ve made any errors, I am not an expert in digital signal processing at all.