At 15:50 Eastern European Time on the 18th of June 2024, I walked out of my last exam, having finally finished school after 13 years. This also meant that I could get into programming again, having been forced to quit my work in favour of studying.

Three days later, I was sent a PDF with the grades I received in my exams. What stood out to me however, was the QR code in the top right. This it what the PDF looks like. (And no this isn’t the real one. In fact, go ahead and scan the QR code, I dare you.)

The only clue to the code’s function is a small text below referencing CycladesVérif, a mobile application. To quench my curiosity I downloaded it and scanned the code. What I got was a summary of my personal information and grades. I would guess the code is for universities or employers to verify that you didn’t tamper with the PDF in order to boost your grades. They provide an example of what it looks like after scanning a QR code on the Play Store:

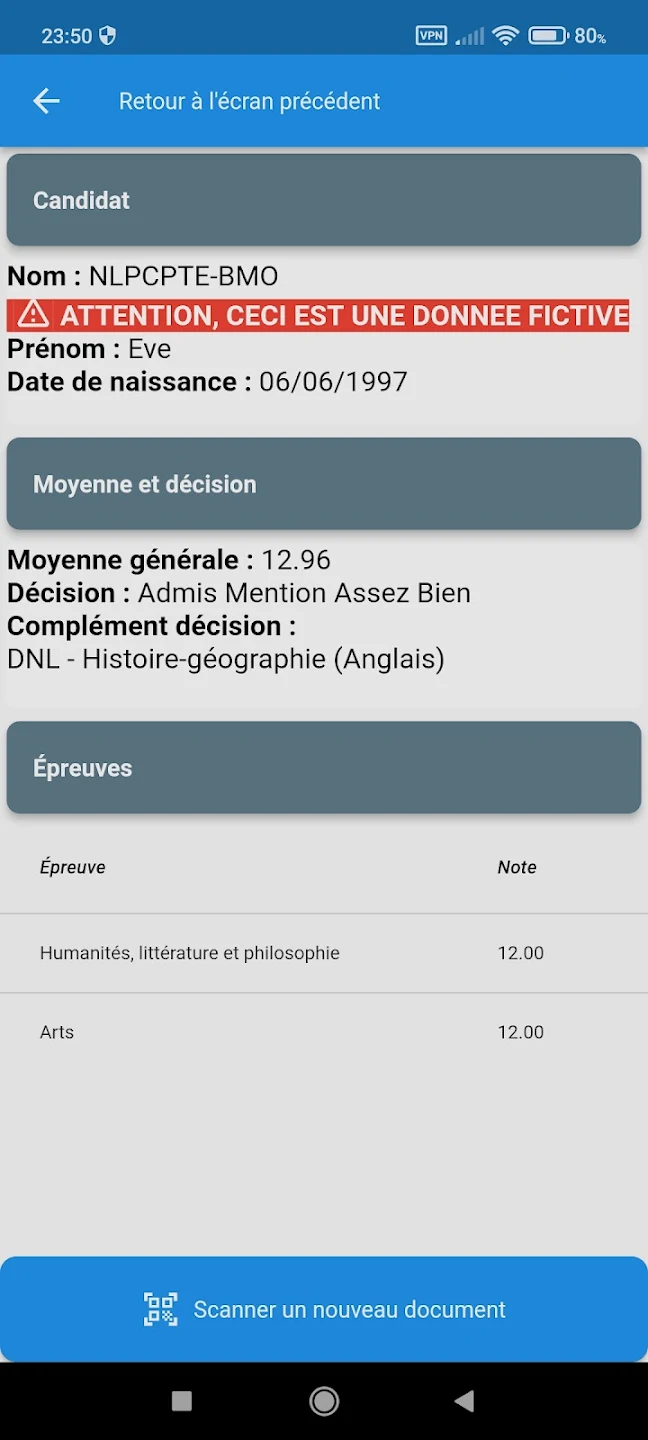
What annoyed me however was that this mobile app - which wouldn’t work on all devices - was the only way to scan this code.

My first naive Attempts

This isn’t the first time I see a QR code that allows verification of data. The Green Pass App that was ubiquitous during Covid allowed authorities or event staff to scan your code to check for up to date Covid tests or proof of vaccination.

These usually work by encoding the data using base64 and appending a signature at the end. In case you are a web developer this works similarly to JSON Web Tokens. The signature is a hash of the data encrypted with an RSA private key. When the user scans the QR code the signature is decrypted into the original hash, which is then compared to a new hash of the data sent in the QR code. If both hashes match, you can be sure there hasn’t been any tampering with the contents. If they don’t, you know you can’t trust the data.

As I have at least a little bit of trust in the French authorities’ knowledge of computer security, I assumed they would not only store the data about the user, but also sign it.

When I scanned the code to extract the data, what I discovered was a simple base64 encoded string (which I knew because it ended in ==) exactly 258 bytes long. But my excitement didn’t last long as the result of decoding it was random bytes that didn’t seem to contain any useful data.

Discovering that this would take longer than I thought

After asking my friend to send me his PDF too, I realised that his was also 258 bytes long. For anyone with a little knowledge about RSA encryption, this does not bode well. But at that time I was blissfully ignorant and assumed I did something wrong - I thought I may have chosen the wrong character set - and it would decode just fine after fiddling with it a bit.

But when I was still left with illegible garbled data, I knew that I would have to look inside the app itself to discover how it accessed the data.

But there was one more thing to try first: Did the app access the internet to fetch the diploma? This would tell me if there was hope for a simple and quick solution. After putting my phone in airplane mode I could still access the data through the app. This was good news, as it confirmed that both the data and the keys to decrypt it had to be in the app itself. But actually accessing them would be another challenge.

Dissecting the App

Armed with the little knowledge of Android apps I had, I looked at the APK, in search of useful Java code.

And Java code I found, but it was mostly gibberish. Anyone slightly familiar with Java knows that what you’re looking for is the MainActivity. But what i discovered in was an empty file.

After a bit of googling I realised something, which should be obvious if you took the time to read the name of the imported package: the app was using Flutter. And after a bit more googling (well a lot more) and 50 Reddit threads later, I knew to look for a file called libapp.so. It should have the (compiled) Dart code for the app, which would mostly be unreadable to humans.

Armed with Ctrl+F I tried to dissect the madness. I was looking for something specific, which was public or private keys and mentions of RSA or other similar encryption schemes. My first search for public yielded the gem ----BEGIN RSA PUBLIC KEY----- between a sea of garbage method names and pointer references.

This meant my suspicions were mostly confirmed. The app uses an RSA public key to decrypt the scanned data and extract the diploma. But to investigate further I would have to get more readable source code. Luckily, a friend of mine who recently finished his course on computer security at university and has published a paper in the field was able to use Ghidra to disassemble the Dart code into assembly.

Digging through Assembly Code

After a lot of searching, I finally found a file that seemed to be responsible for the app’s main functionality. It had the ----BEGIN RSA PUBLIC KEY----- string again and also contained method names like _decodeWithRSAToken.

After a day or two of familiarizing myself with the syntax and different instructions that make up the provided assembly code, I was able to piece together the steps to reproduce what was happening.

1. First the app calls the function scanBarcode() to get the data from the QR code

2. Then, it compares the first two digits to find out which version the document has. It can be either 01, 02, 03 or 04. These two digits account for the first two of the 258 bytes. This means that the encrypted data itself is 256 bytes long. This is exactly the length of the result of encrypting something using a RSA 2048-bit key.

3. Depending on the result of the comparison, it uses a different method and a different public key to decrypt it. My diploma starts with 02 and therefore the apps calls _decodeRlnWithRSAToken2022().

4. This function first creates a PEM version of the RSA token - which means it prepends the ----BEGIN RSA PUBLIC KEY----- and appends the -----END RSA PUBLIC KEY----- suffix to the key. Then it decodes the QR code with base64 and decrypts it with the RSA public key and PKCS#1 padding. The resulting bytes are processed with a Latin1 decoder - Latin1 is a type of text character set, like UTF-8.

5. The decrypted and decoded text is then passed to _transformTextToReleveNotes() and parsed using a Regex that extracts the data and displays it to the user.

After wrestling with the openssl command line tool and invoking a few arcane options, I managed to coax it into correctly decrypting the bytes. The result of the decryption looks like this:

openssl rsautl -verify -inkey key.pem -pubin -in data.bin -raw -hexdump

0000 - 00 01 ff ff ff ff ff ff-ff ff ff ff ff ff ff ff   ................
0010 - ff ff ff ff ff ff ff ff-ff ff ff ff ff ff ff ff   ................
0020 - ff ff ff ff ff ff ff ff-ff ff ff ff ff ff ff ff   ................
0030 - ff ff ff 00 42 61 63 63-61 6c 61 75 72 e9 61 74   ....Baccalaur.at
0040 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX    g.n.ral session
0050 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX    2024|XXXXYYYYY|
0060 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   XXXXXX|XXXXXX|10
0070 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   .00|Admis Mentio
0080 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   n Tr.s Bien avec
0090 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX    les f.licitatio
00a0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   ns du jury||Epre
00b0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   uve orale termin
00c0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   ale (Grand oral)
00d0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   ~10.00#Math.mati
00e0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   ques~10.00#Physi
00f0 - XX XX XX XX XX XX XX XX-XX XX XX XX XX XX XX XX   que-Chimie~10.00

From which we can extract the following text, using the Latin1 character set and parse it with the regex:

Finally, in the _transformTextToReleveNotes() function, the grades at the end are separated by at the hashtags # and then the tildes ~ to parse and display them to the user.

Using this information, I wrote a Python program that extracts my data from the PDF.

Using RSA creatively to sign physical documents

Encrypting with the private key and decrypting with the public key is usually only done in the context of signing/verifying. This is consistent with the \x00\x01 bytes at the beginning of the decrypted message’s padding. The \x01 byte indicates a block type 1 in PKCS#1 padding, which means the operation performed was signing.

Python’s cryptography libraries straight out refuse to do any decrypting with public keys, the only available methods are for verifying. This requires you to provide the signature and the message. This is not possible here, since the signature is the message. Thus I had to resort to the obscure openssl commands and in the case of my Python program, had to reimplement the RSA algorithm in Python to get useful results.

EDIT: However, this is not what is happening here. After posting this to Hacker News I got some valuable information from people obviously more knowledgeable than me.

According to this comment using RSA to encrypt the whole message in the signature is called “signature with (total) message recovery”. But according to the RFC (the official document outlining how RSA should be used) this is not intended functionality:

Accordingly, the EMSA-PKCS-v1_5 encoding method explicitly includes a hash operation and is not intended for signature schemes with message recovery. - RFC 8017, Section 8.2

EDIT 2: Thanks to a very helpful commenter on Lobsters I stand corrected. In this scenario and for this threat model, signing with total message recovery is an accepted practice. As this Stack Exchange reply states there are ISO standards for it. But verifying if it was done correctly here is out of reach for me.

As I understand it, the reason signature with message recovery is not recommended is because it creates the possibility of an attacker generating a random string that decrypts to valid data.

The good news for the French ministry of education is that it’s probably not possible to forge a diploma, as we’ll see in this next section.

What’s the Probability to randomly generate a valid Diploma

In order for the App to actually show data instead of exiting, we need the decrypted text to match the regex. The simplest possible text which is valid is the following, because it has the 8 | pipe separated sections and the birthday. The pipes don’t actually have to have any text between them, as .* matches any character between zero and unlimited times.

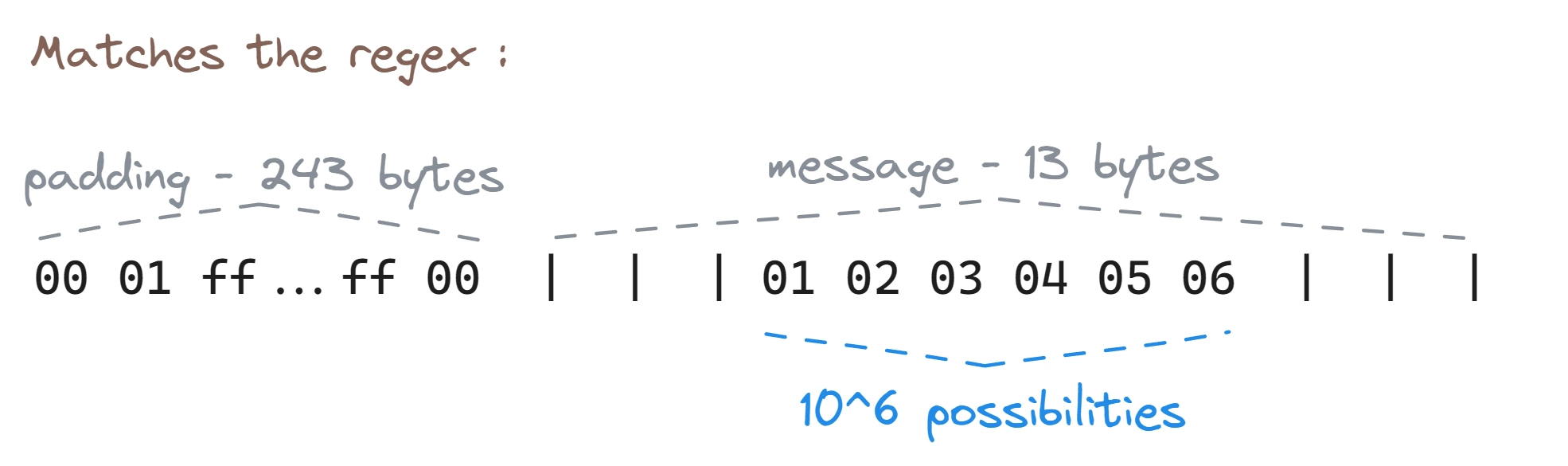
This means that we can calculate how many possible messages there are, that match this regex.

If there are 243 bytes of padding (\x00\x01\xff... 238 more times ...\xff\x00), then we have $10^6$ valid messages. This is because the birthday has 6 characters, which can be digits from 0 to 9. Every other bytes has to be a specific value in order to match the regex.

But as soon as we use only 242 bytes of padding, we have one character that could be anything, and can be located anywhere between the pipes:

And since the app uses the Latin1, there are 189 valid characters that byte could represent.

To calculate the amount of possibilities for $n$ chars (so $256 - 13 - n$ bytes of padding or $13 + n$ bytes of message) we have to consider how many ways we can put the $n$ chars in the spaces between the pipes. This is solved by the classic combinatorial formula called the stars and bars theorem. It calculates the number of ways to place $n$ indistinguishable balls into $k$ labelled urns.

We can use python to sum all possible combinations for us:

import math

def distinct_distributions(n, x):
    # Using the combinatorial formula for stars and bars
    return math.comb(n + x - 1, x - 1)

total_possibilities = 0
for n in range(0, 256-13):
	total_possibilities  += (189**n) * distinct_distributions(n, 7)
total_possibilities  *= 10**6

But we want to know if there is any chance for us to generate one such message by checking all possible encrypted ciphertexts iteratively. The total number of existing ciphertexts is $256^{256}$, because they have to be exactly 256 bytes long. By diving $256^{256}$ by the amount of messages which match the regex, we know how many we would have to try on average, before finding a single valid one.

minimum_checks = 256**256 // total_possibilities 
print(f"How many decryptions to perform before finding one which validates the regex: {t}")
# How many decryptions to perform before finding one which validates the regex: 
# 1319814855853530981336893039920992872421595910518

That is a lot. To calculate the necessary time to test all of these, I use the speed of a C program I wrote that creates a ciphertext, decrypts it and tests for matches. It can perform 100k checks in 2.39 seconds.

speed = 100000 / 2.39
print(f"Checks per second {v}")
# Checks per second
# 41841.00418410041

time = (minimum_checks / speed) / 60 / 60 / 24
print(f"Days to find one result: {time }")
# Days to find one result:
# 3.650876742465208e+38

$3 \cdot 10^{38}$ days is a completely unrealistic timespan, so we will sadly have to surrender to the French…