Niklas Oberhuber

An attempt will be made to find how to make machines use language, form abstractions and concepts, solve kinds of problems now reserved for humans, and improve themselves. We think that a significant advance can be made in one or more of these problems if a carefully selected group of scientists work on it together for a summer. - J. McCarthy, Dartmouth AI workshop proposal, 1955

Turns out, it wasn’t actually that easy. A few years before the workshop, in 1949, Alan Turing devised the Turing test, which measures a machine’s capabilities of using language. We now have, 75 years after it’s creation, empirical proof of machines passing a rigorous Turing test in a controlled setting, with 73% of judges mistaking GPT-4.5 for a human. That’s exactly 139 summers more than J. McCarthy thought.

We’ve come a long way since the simple lookup-table-like system developed for ELIZA in 1966 (which did not pass the Turing test). I attempted to sum up my research into techniques used for language models in this post.

Markov Chains

Claude Shannon, one of the original attendees of the Dartmouth summer workshop used Markov Chains to approximate text in his 1949 paper A Mathematical Theory of Communication. While he worked with character level Markov chains, we’ll also consider word and token level chains.

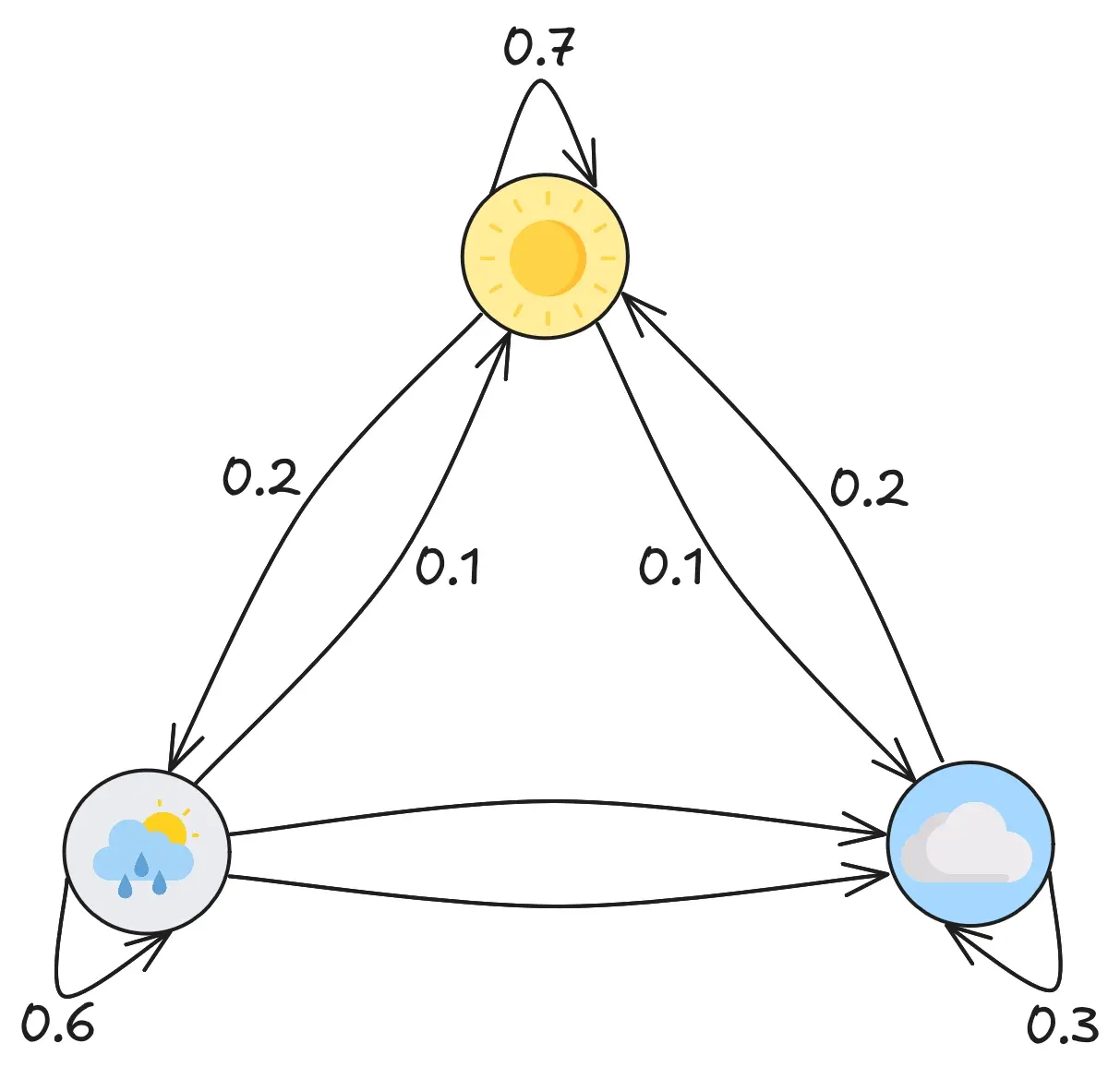
Markov Chains model stochastic processes. They model the way a random system - the weather for example - evolves from one state to another. If it’s sunny, there’s then a certain probability for cloudy, and from cloudy it’s more likely to get rainy. A Markov chain can be “trained” on a set of examples to approximate these probabilities.

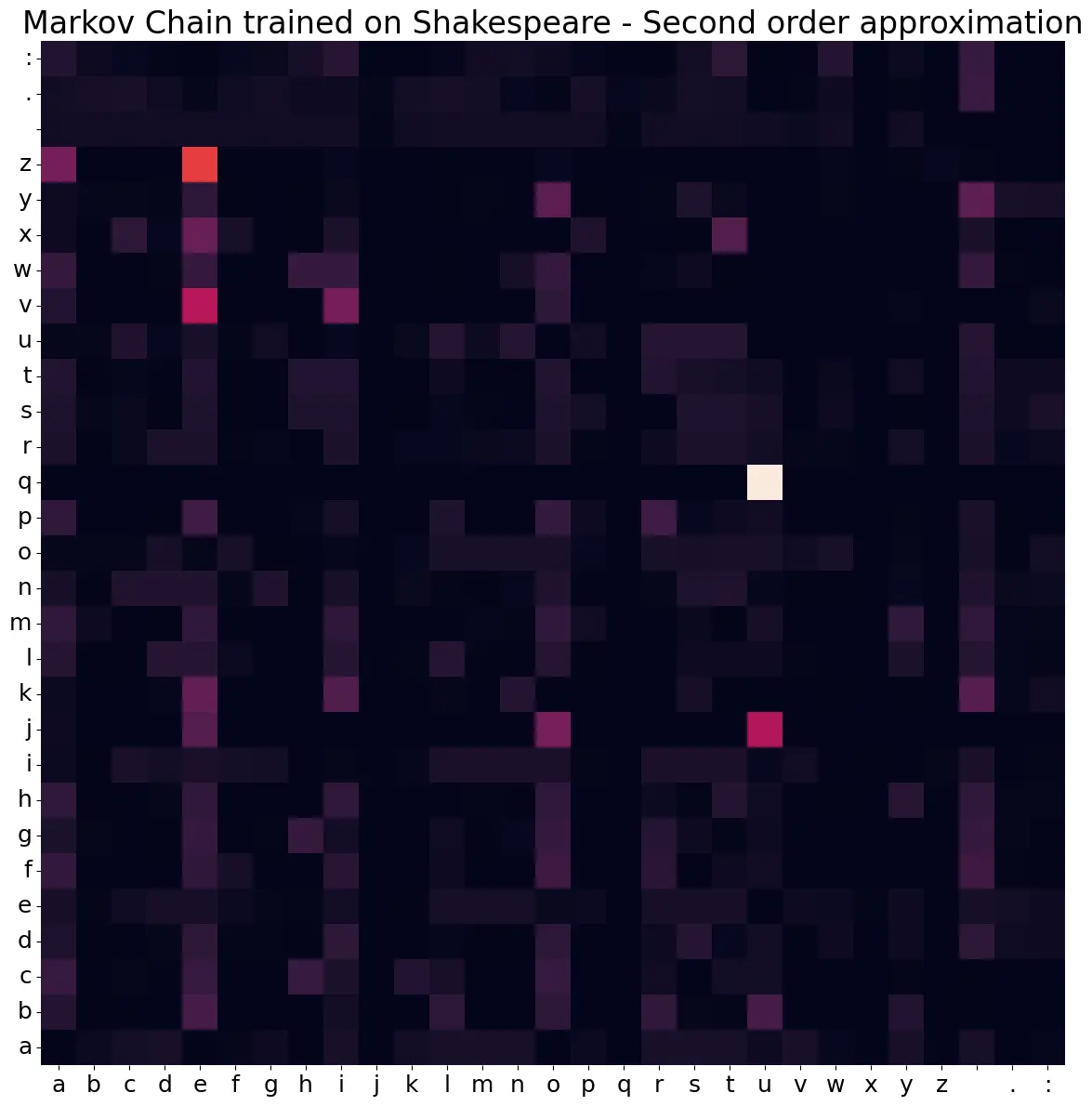
Because Markov Chains are essentially directed, weighted graphs, they can be visualised as matrices. The following heatmap shows the probability of a character appearing after another. Notice for example, that after q there is almost always a u.

The output of a model like this is essentially gibberish (text like “dw ci onerey gomilver” won’t exactly convince human judges in a Turing test) as knowing the single preceding character isn’t very useful to predict the next.

We can increase the size of the context (order of the model) to 3, 4 or even 6 characters, which of course massively increases the memory footprint of our markov chain matrix. The size of the Markov Chain grows $O(k^n)$ which makes it impossible to provide more than a few dimensions of context.

There’s also the issue that, as we give more and more context, the output will slowly approximate the training corpus. This is especially noticeable for word-level chains, as n-grams of 4 or 5 words will be highly unique in a moderately sized text.

Byte Pair Encoding

Training a Markov Chain on character level data has the consequence that the model can (and will) produce anything (from these characters). That is just a bit too much freedom to generate useful text. Using word-level data is a big constraint, as the model will never be able to generate any “new words” or declinations. It’s entirely limited to the words that were in the training corpus.

This is where tokens come in. They serve as a nice middle-ground between characters and words as they are usually more like syllables. You don’t get complete gibberish, but not all freedom has been removed. LLMs operate on token level data, you can play with GPT tokenizers on their website.

The state of the art tokenizing algorithm is called byte pair encoding (BPE). A very readable implementation was provided by Andrej Karpathy with minBPE. The basic premise of BPE is the following:

1. Split the input into individual characters.

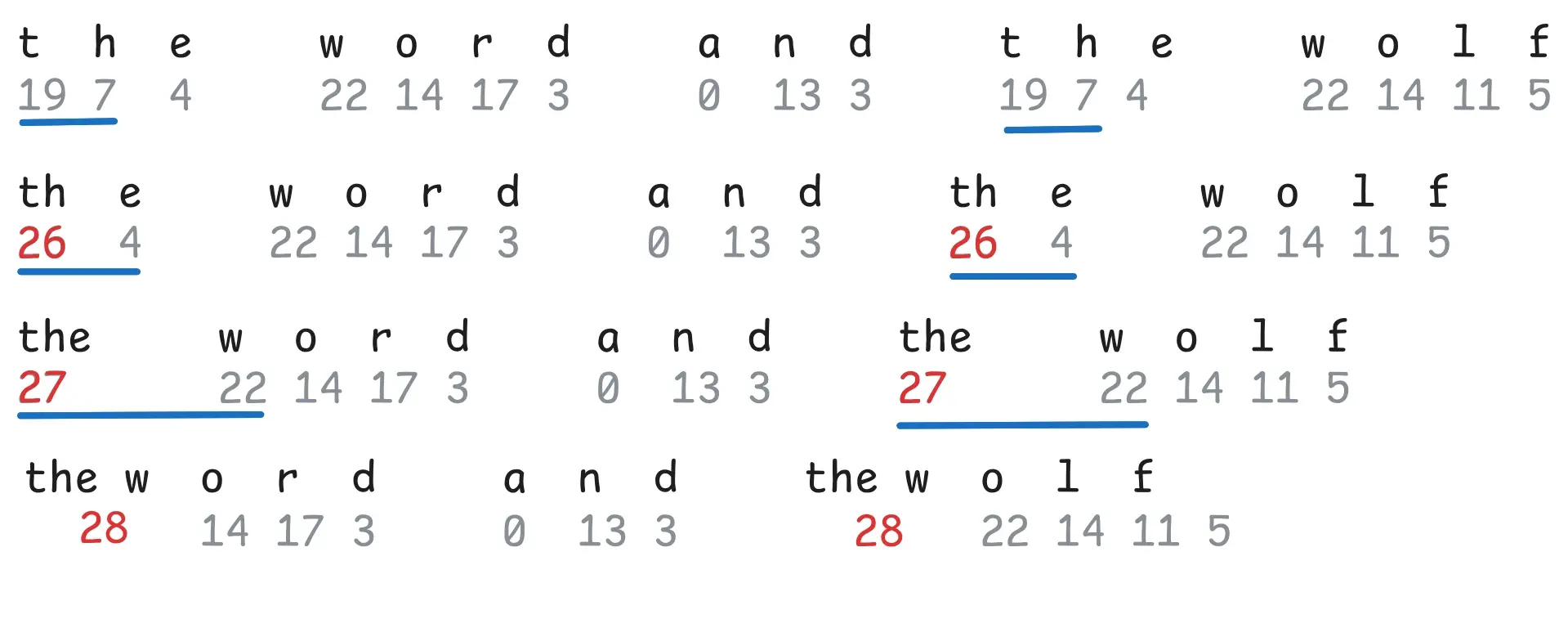
2. Go through the entire input in groups of two and count the occurrences of pairs.

3. Take the most frequent pair and merge it (q and u becomes qu) and add it as a new token.

4. Repeat from step 2. for the new list of tokens.

Less frequent combinations will be represented using smaller tokens. BPE also doubles as a compression algorithm.

Applying BPE to the same dataset used above, produces tokens like ing, for, and, etc… The output is still meaningless, but it looks more like actual human language and isn’t a word for word reproduction of the corpus, all using only a single token of context: first citizen: “prithee now arrestthe otherincious lowd friendsthis doublecall”.

GPTs

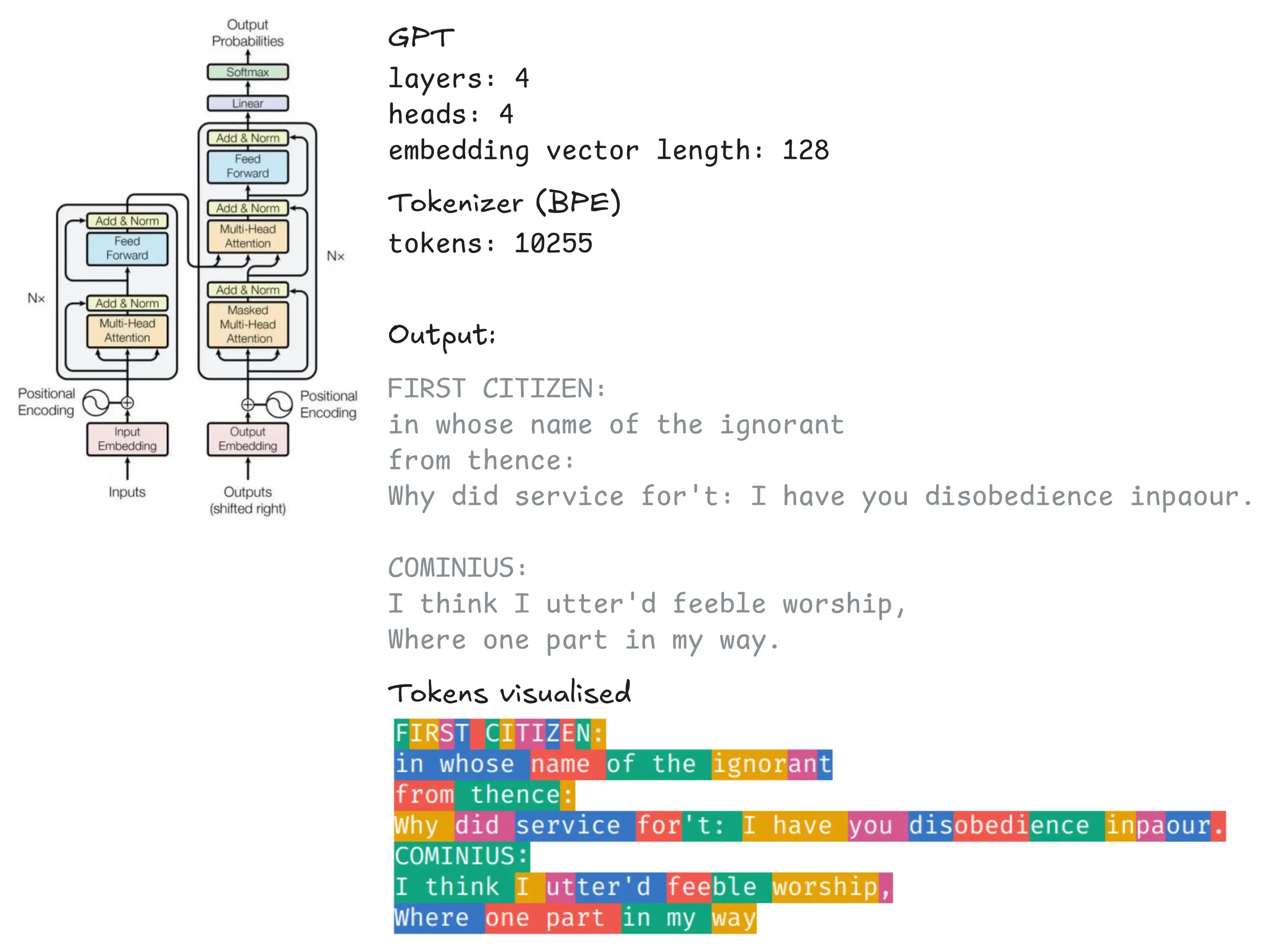
Now that we are operating on tokens, we’re essentially pretty close to modern LLMs. When we are working with a context of two or three tokens, they are all weighted equally, which is not ideal. Instead, we would like to change the output probabilities based on the current word and how it relates to those before it.

This is what LLMs do. A generative pre-trained transformer uses a mechanism known as self-attention to assign weights to the words in the context and have them interact with each other. Check out Amanvir’s visualisation of the different attention heads in GPT-2 to get an intuition for this process. I also highly recommend checking out Andrej Karpathy’s minGPT to understand GPTs.

After training a small GPT on the same Shakespeare text as before, tokenized into 10255 tokens with my re-implementation of Karpathy’s minBPE, we get the following results.