Niklas Oberhuber

Nerd-sniping me is pretty easy. Step 1 is to get me a board game. Step 2 is to beat me over and over (at the game, not literally please). This will give me the necessary motivation to build a program in order to take back my dignity…

Meet Today’s Victim

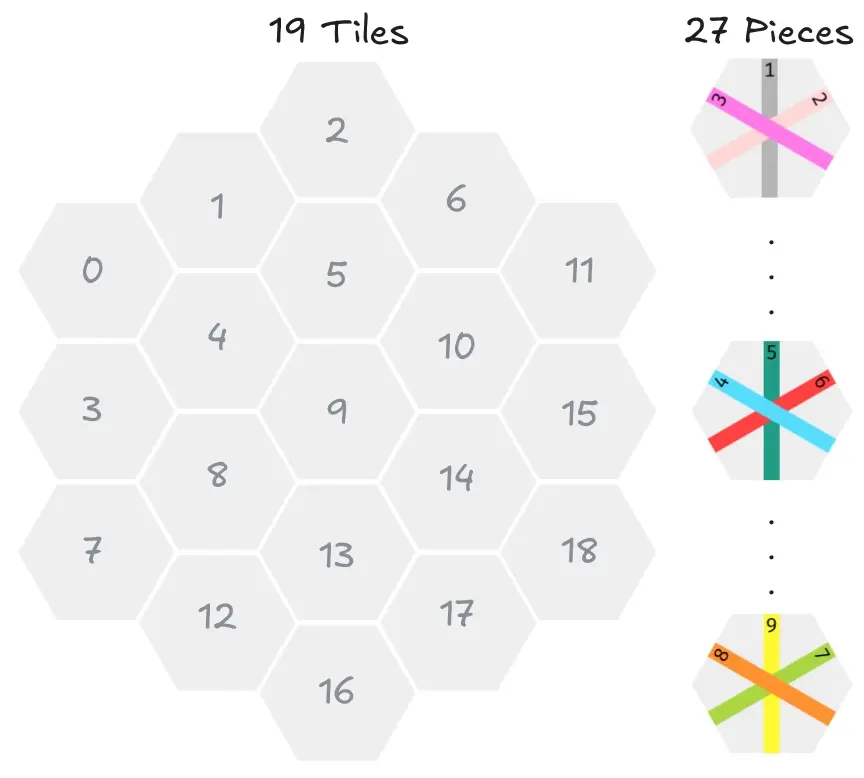
Take It Easy is played on a hexagonal board with 19 tiles and a stack of 27 pieces. Each turn the player draws a random piece from their stack and places it on an open tile on the board. The goal is to score the highest number of points.

Each piece has three lines on it, one vertical, one diagonal from left to right (LR) and one from right to left (RL). There are three different “line values” per direction: the vertical line can be worth either 1, 5 or 9, the diagonal LR 3, 4 or 8 and the diagonal RL 2, 6 or 7.

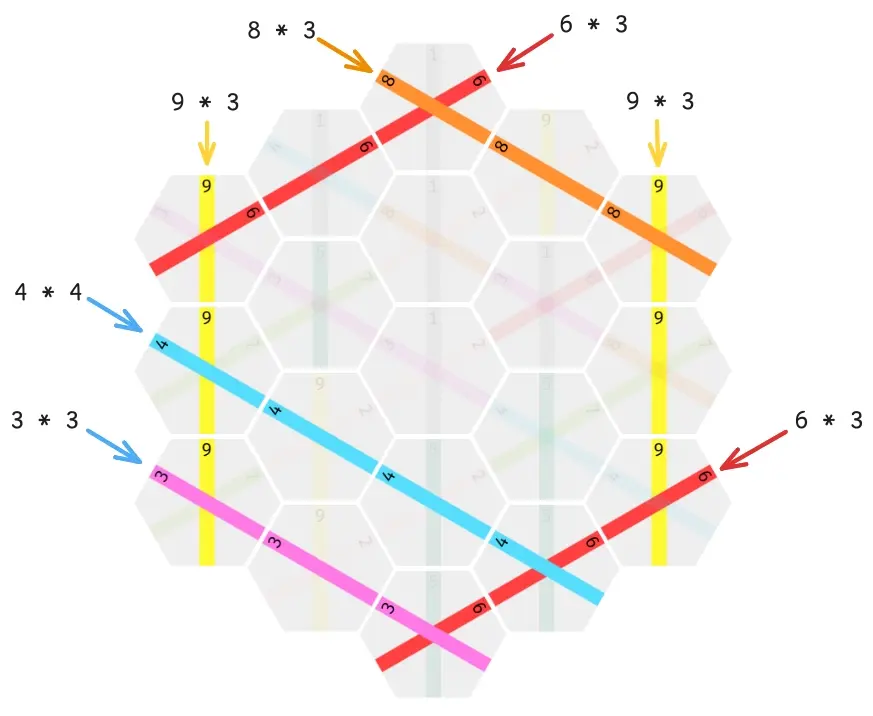
A completed line - meaning a fully connected path going vertically or diagonally from one end of the board to the other - is worth it’s length times the value of the line. The maximum possible score is 307, which can be achieved in only 16 different ways.

If you want to take a shot at playing yourself, go to take-it-easy.obrhubr.org. See if you can beat the AI!

First Attempts

The game cannot be deterministically solved due to the huge state space. With 27 tiles, 19 of which are drawn each game and can be placed anywhere on the 19 tiles, there are $\approx 2.7 × 10^{23}$ possible games, which is simply too much to fully explore.

To establish a baseline performance, we’ll compare different basic strategies. A bot playing random moves only (plot 1) will score mostly 0.

A greedy bot that places pieces randomly except if it can complete a line halves the number of games scoring 0 and ups the mean to 23 points (plot 2).

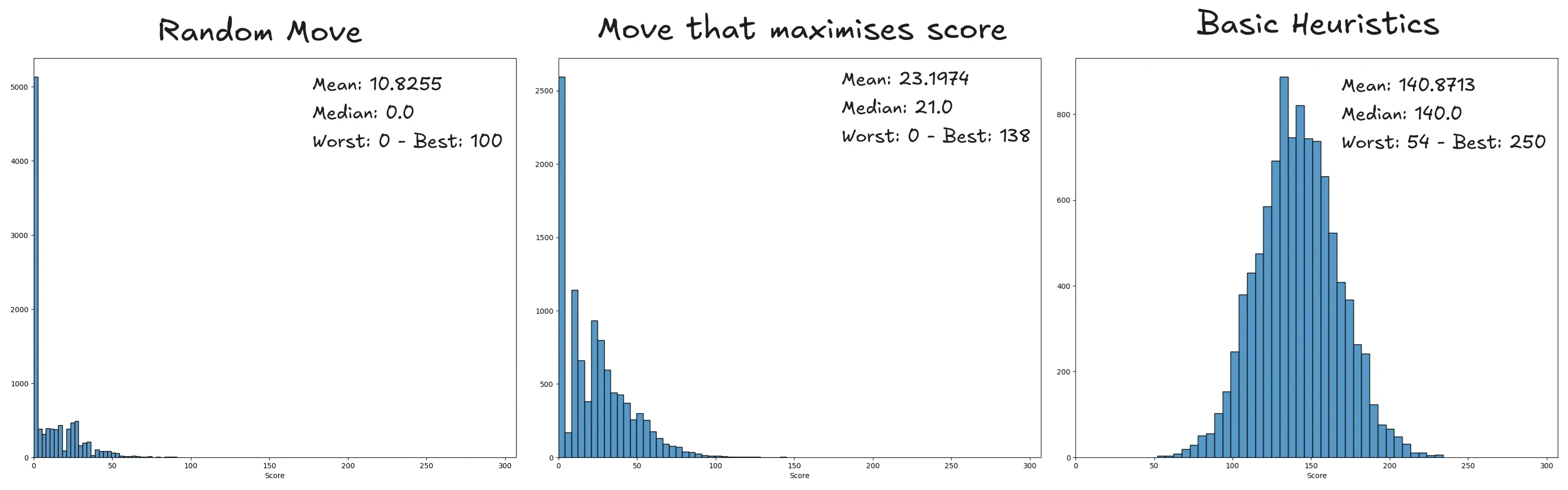
To improve on that score, I wrote an evaluation function that captures the potential value of an uncompleted line. This basic heuristic scores lines that have a good chance of being finished higher than those that are already blocked, according to the number of pieces with the right line on them left.

This upgrade increases the mean score to about 142 points and completely eliminates 0 point games (plot 3), which is a massive improvement. But we can do better…

A Neural Network Based Approach

After struggling to come up with better heuristics for a while I embraced the Bitter Lesson and looked into NN based techniques.

After fooling around for a bit, I gave up due to my limited knowledge and searched for some prior work. I found polarbart’s awesome bot, which I re-wrote and explored in depth as a learning experience.

Here are the final scores, which easily beat my previous bots.

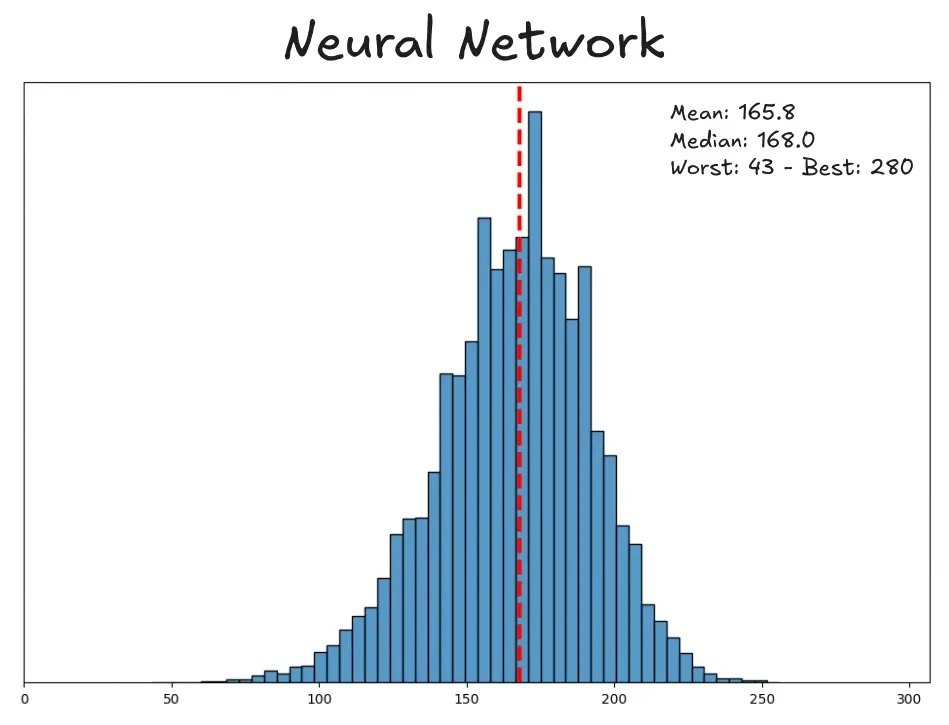
About a hundred hours of training and a significant jump in computational complexity gets us a median score of 168 points (28 more than the basic heuristics). The best score achieved also increases from 250 to 280.

Inference

Instead of manually writing an evaluation function like before, the bot has a neural network score the board. This technique is a type of Q-Learning: the next move is not only chosen based on immediate reward but also future rewards.

In the case of Take-It-Easy, the neural network spits out a probability distribution for the expected final score. This approach works so well because the distribution manages to capture the randomness of the game better than just the usual single score (see the paper referenced by polarbart).

Training

But the model has to learn to accurately estimate the probability distribution somehow… To make things even more difficult, Take-it-Easy gives us only limited immediate feedback (the reward for completing a line) while the final score can only be calculated at the end.

The Bellman equation allows us to bridge the gap between reward and final score. The evaluation function $\mathbb{Z}$ is updated according to the immediate reward $r$ and the probability distribution of the next state (according to optimal policy) noted $\mathbb{Z}(s')$.

If you’re not at all used to the industry jargon, this may sound mostly like magic words (I certainly was very confused). In practice this means that during each round of training the model plays a lot of games. To update the NN, we train it on the current state as the input, with reward + probability distribution of the best next state as the output. Thus, with every move, we encode another tiny sliver of information (the reward).

The model kind of bootstraps itself, as each iteration learns from the previous one. Seeing this in action kind of felt like magic to me.

Limits

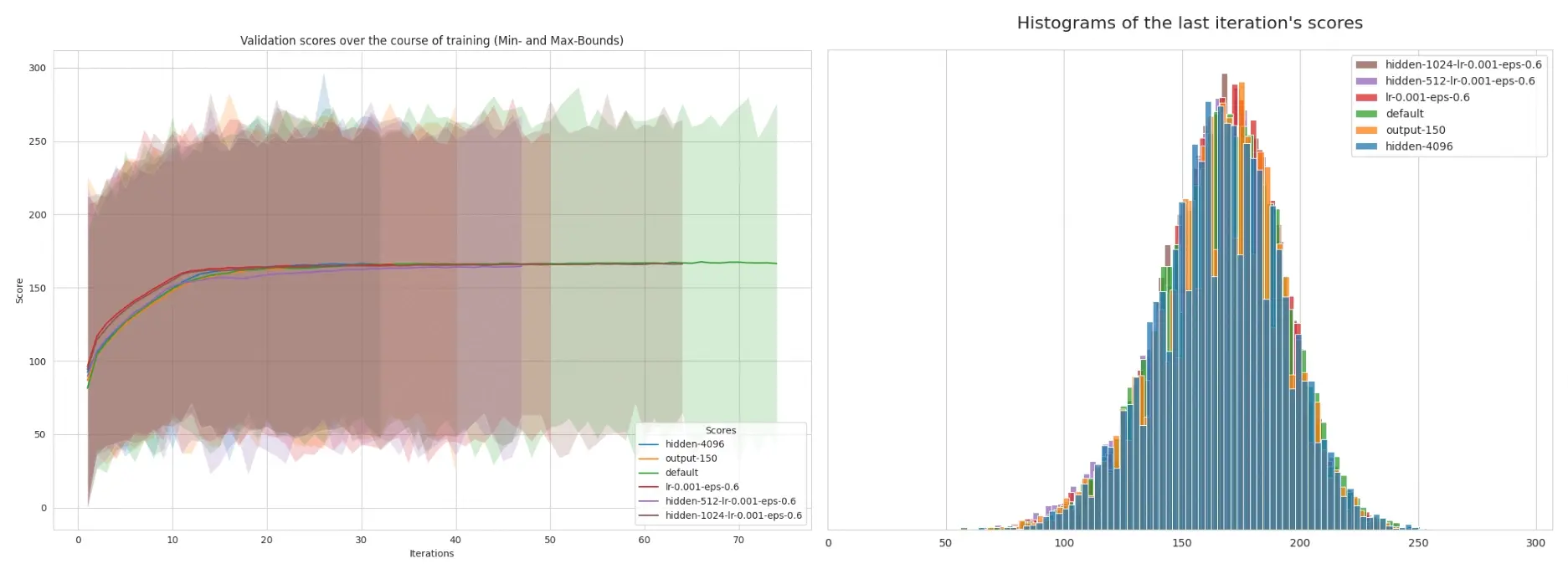
While experimenting, I trained many model configurations, varying different parameters: hidden size, learning rate, epsilon, output size, dataset size, etc…

The results were all pretty consistent. Changes in any of the parameters didn’t affect performance and only reduced or increased the rate at which the model improved initially. But all models eventually hit the seemingly hard limit of ~167.

I wasted at least a couple hundred hours and a pretty sum renting GPUs for training, all in a futile attempt to increase the score (If you want to take a shot at training your own model, I provided a Colab notebook).

This hard limit on the score could either be the result of a pretty huge local minima that halts progress, or it could be evidence of the natural entropy of the game itself.

Similar to how an LLM can never be sure if the next word in the sentence “The house stood upon a“ is (it might be hill, mountain etc…) due to the natural entropy of language, there might not be a single optimal move in Take-it-Easy.

This intuitively makes sense: the random order of the pieces drawn means that there is never a “best” move. The game could just be too random for a player to achieve more than 167 points on average, even with the best possible strategy?

Interpreting the Trained Model’s Parameters

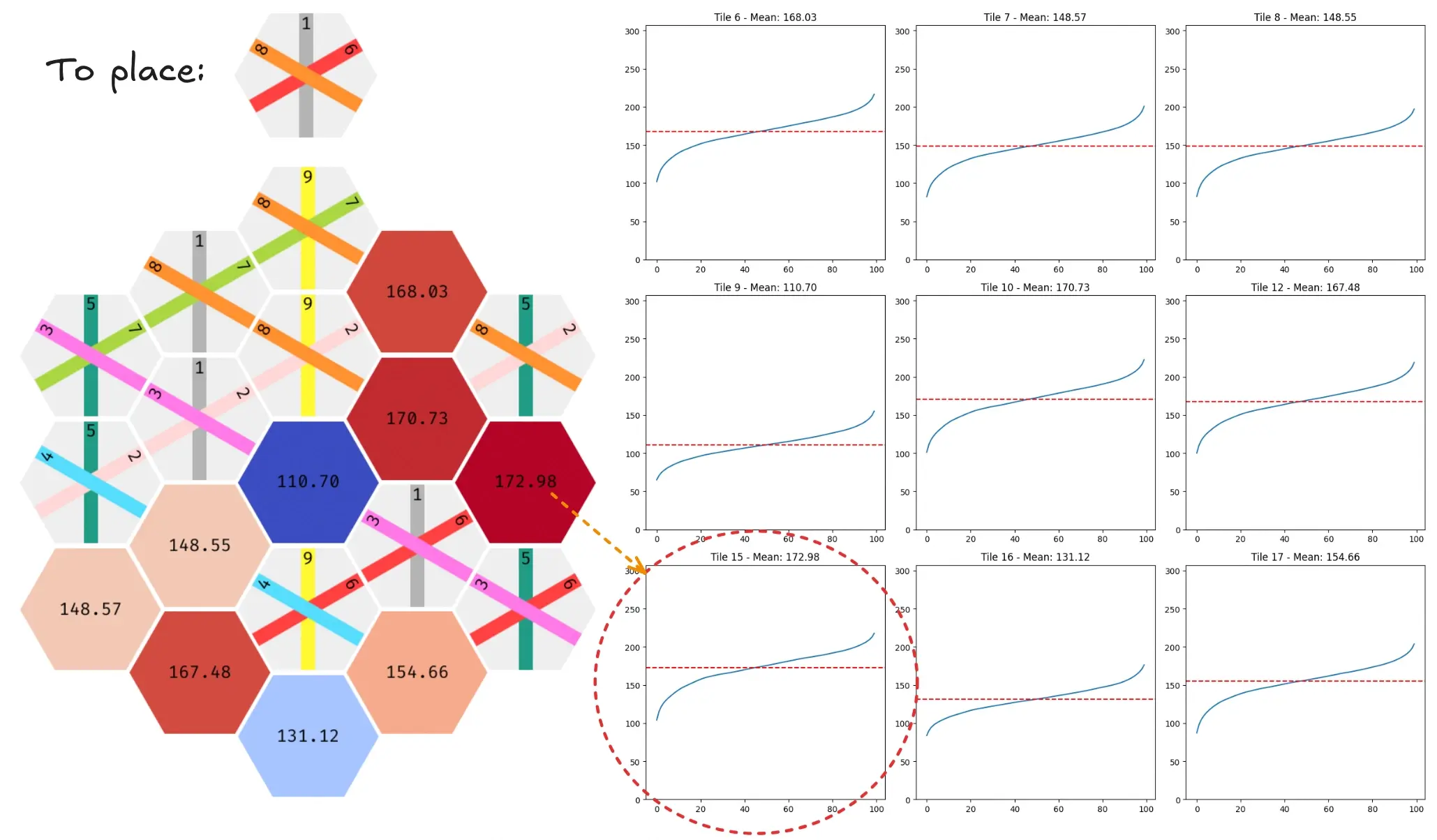
I wanted to find out more about the strategies employed by the different models, in order to find out if they converged - and got stuck on - a consistent strategy. To visualise what effect on the score placing a piece on a tile would have, I mapped each input neuron’s weights to their corresponding tile and line on the board.

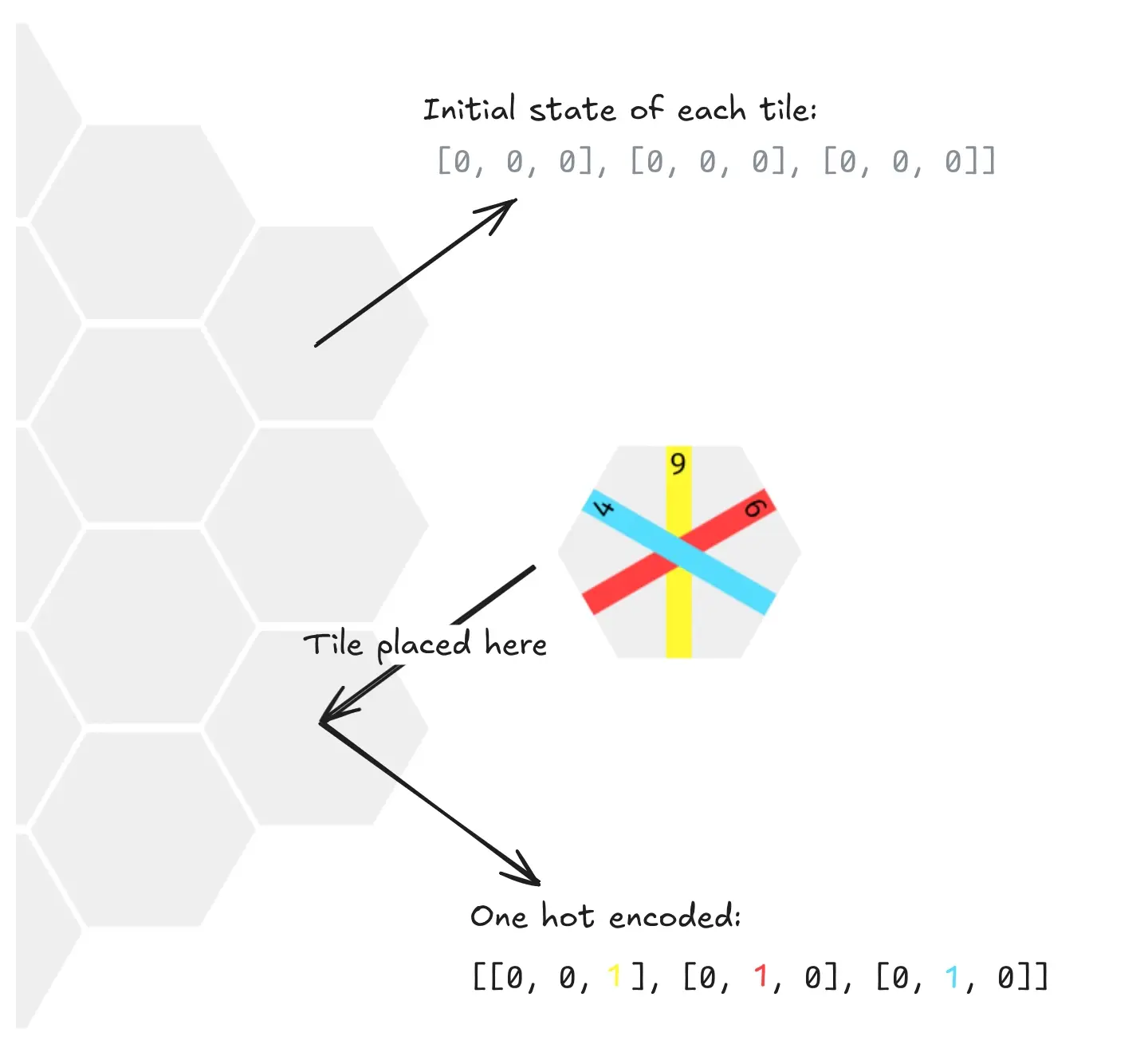
The mapping from board to neural network input is based on one-hot encoding. For each tile, we encode 9 bits of information about the piece on it: three lines per tile and three possible line values for each of them.

A red line means that placing a piece with that line on this tile influences the model’s first layer positively, while a blue line means the next layer is negatively influenced.

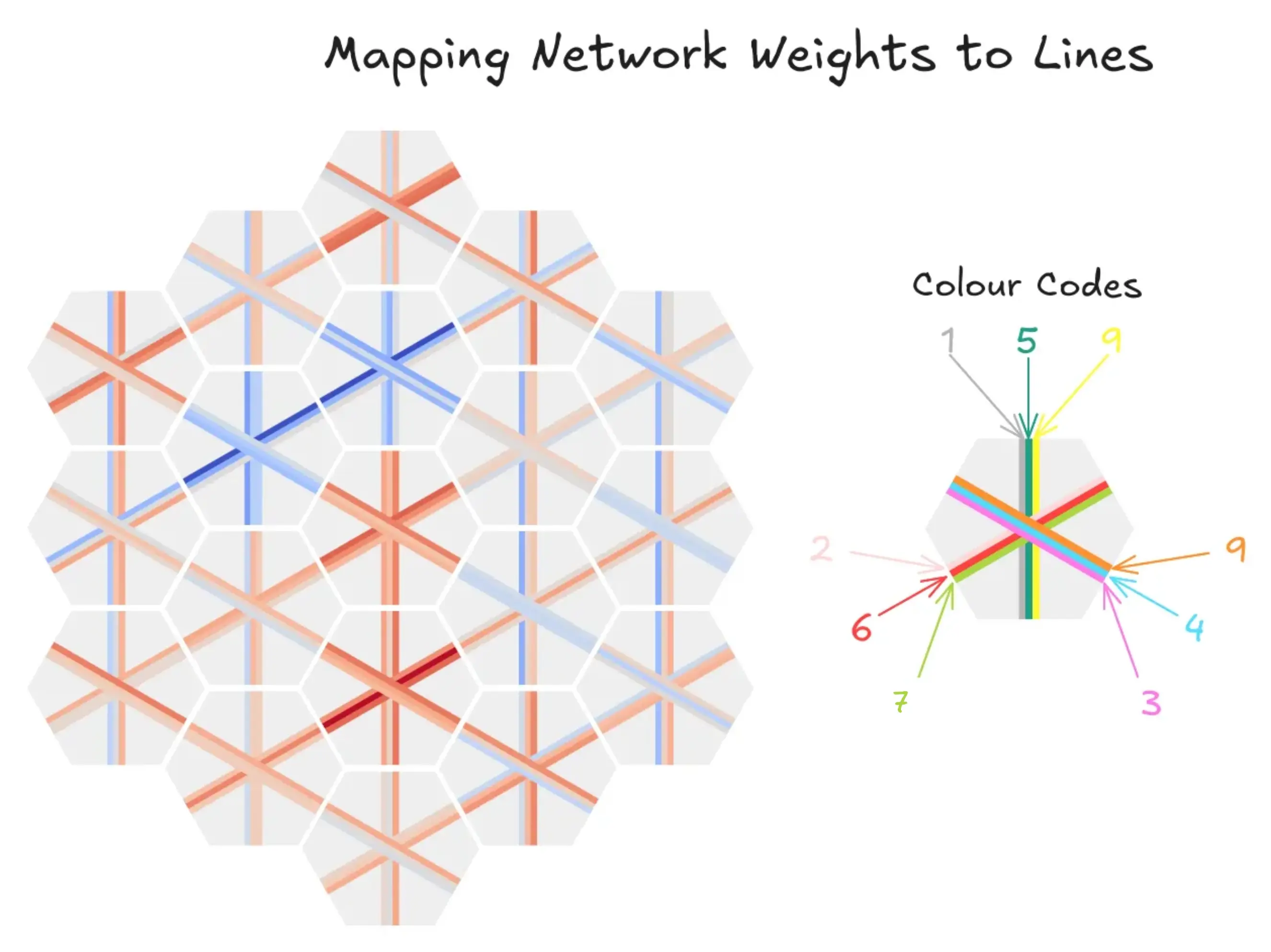
What is interesting is that the mapping of weights to lines is not at all universal. Every model shows a different pattern when visualised this way. This might be due to this not being a very reliable test, or…

The actual predicted score of the same board stays consistent (a few points maximum), no matter the model configuration. Therefore, this might be another clue that there isn’t a single best strategy and that Take-It-Easy is too random to score more than ~167 points on average.

Open Questions

Going through polarbart’s code in detail, slowly reconstructing his model architecture and fiddling with different optimisations (or un-optimisations because of a lack of understanding…), helped me gain a lot of insights into this type of reinforcement learning. But there are a few things I don’t understand and maybe by sharing I’ll get an answer.

For those not familiar with loss metrics, usually loss starts out high, as the model quickly adapts to the training data, and then slowly reaches a minimum, not improving any further. Here, because of the constantly changing policy, like a moving target, the loss increases.

The loss staying high after its initial climb seems to further indicate that the game is truly capped at about 167 points due to randomness.

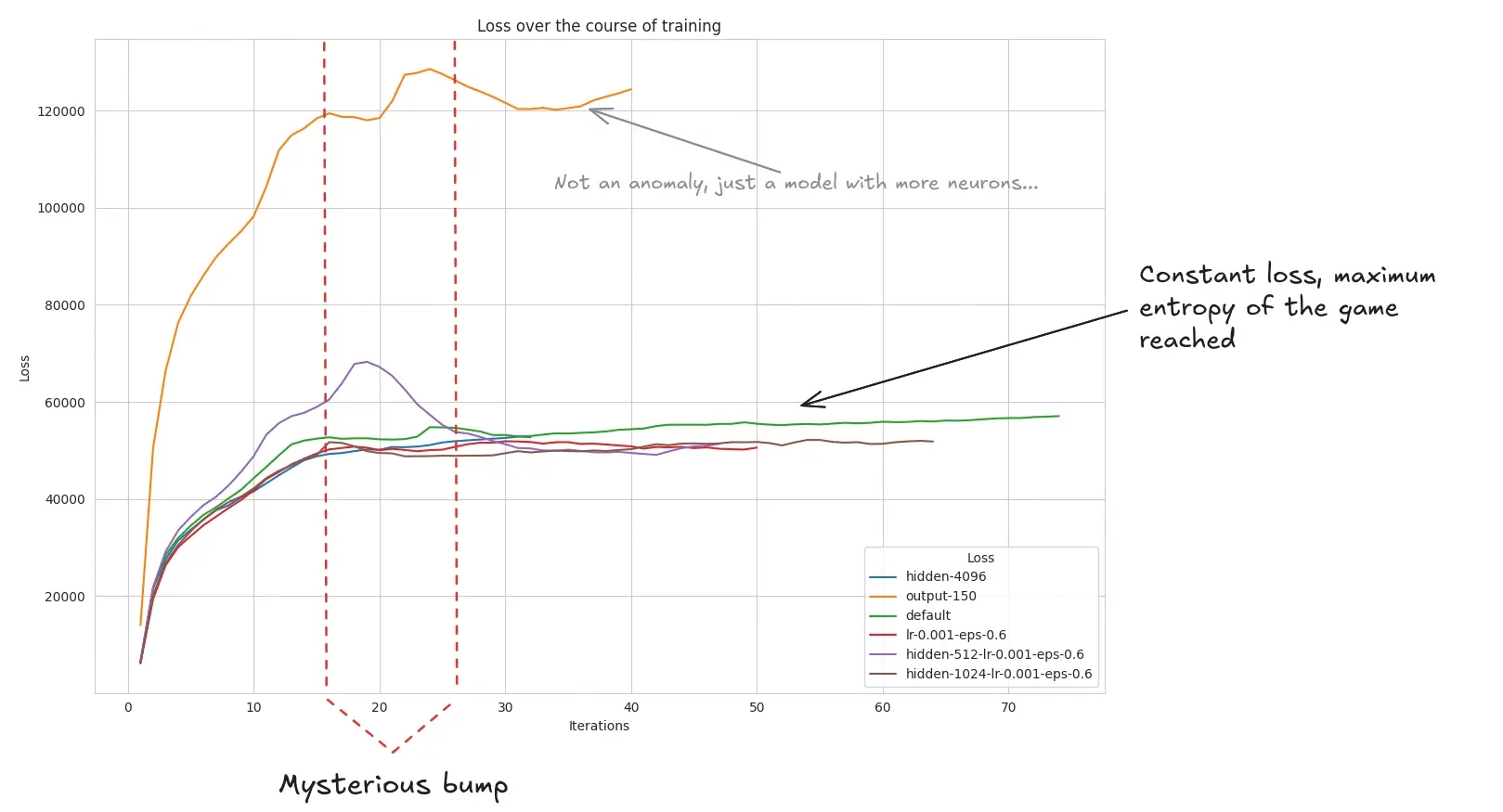
What stood out to me is the small bump happening consistently across model configurations around iteration 20. It might be a critical turning point in model policy, or something else entirely? I would be very interested in an explanation (see my email below)!